
Zadanie Termity 2 (ted)
Pomóż nam usprawnić bazę zadań!
Termity 2
Limit pamięci: 128 MB
Czy pamiętasz jeszcze dwa przyjacielskie sztachetożerne termity, którym nigdy nie dość rozrywek umysłowych? Otóż po spałaszowaniu większości płotów w Bajtocji nabrały apetytu na drzewa.
Drzewem nazywamy spójny graf nieskierowany o  wierzchołkach i
wierzchołkach i  krawędziach.
Naszym dwóm termitom prędko znudziło się monotonne zjadanie wierzchołków - wymyśliły zatem grę,
którą planują urozmaicić sobie posiłek.
Ustaliły pewną kolejność
krawędziach.
Naszym dwóm termitom prędko znudziło się monotonne zjadanie wierzchołków - wymyśliły zatem grę,
którą planują urozmaicić sobie posiłek.
Ustaliły pewną kolejność  krawędzi drzewa, które zamierzają zjeść.
Gra potrwa co najwyżej
krawędzi drzewa, które zamierzają zjeść.
Gra potrwa co najwyżej  rund, w każdej rundzie ruch wykonuje dokładnie jeden termit.
Gracze ruszają się na przemian (zaczynający gra w rundzie
rund, w każdej rundzie ruch wykonuje dokładnie jeden termit.
Gracze ruszają się na przemian (zaczynający gra w rundzie 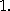 , drugi w rundzie
, drugi w rundzie 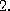 ,
w rundzie
,
w rundzie 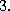 znów pierwszy, i tak dalej).
W
znów pierwszy, i tak dalej).
W 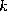 -tej rundzie grający termit musi wybrać dowolny z niezjedzonych końców krawędzi
-tej rundzie grający termit musi wybrać dowolny z niezjedzonych końców krawędzi 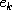 i go zjeść.
Jeśli oba końce
i go zjeść.
Jeśli oba końce 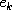 są zjedzone, zanim termit wykona swój ruch, gra kończy się jego przegraną.
Jeśli gra nie skończy się w ciągu
są zjedzone, zanim termit wykona swój ruch, gra kończy się jego przegraną.
Jeśli gra nie skończy się w ciągu 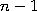 rund, ma miejsce remis.
rund, ma miejsce remis.
Zakładamy, że (doświadczone przecież w tego typu zabawach) termity grają bezbłędnie, przy czym termit, który ma strategię umożliwiającą mu zwycięstwo, dąży do wygranej w możliwie najwcześniejszej rundzie, zaś jego przeciwnik chce przegrać jak najpóźniej. Twoim zadaniem jest, dla danego drzewa i kolejności jego krawędzi ustalonej przez termity, określić, w której rundzie skończy się gra.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita  (
(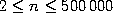 ) - liczba wierzchołków drzewa.
W kolejnych
) - liczba wierzchołków drzewa.
W kolejnych 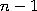 wierszach podane są krawędzie drzewa w kolejności ustalonej przez termity.
W
wierszach podane są krawędzie drzewa w kolejności ustalonej przez termity.
W 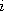 -tym z tych wierszy znajdują się dwie liczby całkowite
-tym z tych wierszy znajdują się dwie liczby całkowite 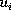 oraz
oraz 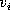 (
( ) - numery końców krawędzi
) - numery końców krawędzi 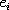 .
.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia należy wypisać jedną liczbę całkowitą
- numer rundy, w której skończy się gra, lub 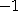 , jeśli będzie miał miejsce remis.
, jeśli będzie miał miejsce remis.
Przykład
Dla danych wejściowych:
5 2 3 1 2 4 5 3 4
poprawną odpowiedzią jest:
4
Wyjaśnienie do przykładu: Jeśli w pierwszej rundzie zaczynający termit zje wierzchołek 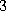 ,
zaś w trzeciej rundzie wierzchołek
,
zaś w trzeciej rundzie wierzchołek  , jego przeciwnik nie będzie miał żadnego ruchu w rundzie
czwartej, niezależnie od tego, jak zagrał w rundzie drugiej.
, jego przeciwnik nie będzie miał żadnego ruchu w rundzie
czwartej, niezależnie od tego, jak zagrał w rundzie drugiej.
Autor zadania: Jakub Pachocki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English